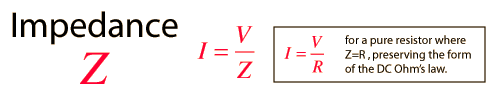Blog Description

This blog contains the summarized topics discussed in Electric Circuit 1.

Recent Posts

Unordered List

Definition List

Pages

Pinapagana ng Blogger.

Ads 468x60px

Social Icons

Featured Posts

Week Five: Sinusoidal Steady-State Analysis Part II

Lunes, Disyembre 22, 2014 | by Unknown

Mesh Analysis

          -The mesh current method of analyzing ac requires Kirchhoff's Voltage Law to sum ac voltages around a closed path in terms of the mesh (loops) current variables. The branch impedances are represented by complex numbers, each with a real part and an imaginary part. the real part represents the branch reactance.

Important Notes:

  • Just as in KCL, the KVL analysis also applies to phasor and frequency domain circuits.
  • The same rules apply: Convert to frequency domain first, then apply KVL as usual.
  • In KVL, supermesh analysis is also valid.

Example: Solve for Io:




For another Example, Watch this Video!


Reflection:
        In applying mesh analysis in ac, the process for solving an unknown are still identical. The only difference is that the values given may occur complex numbers and phasor form for sources. Sometimes, I fail to acquire the correct answer because I carelessly convert the values in their wrong convertion or equivalence. For me, I find mesh analysis more convenient than nodal analysis. But of course, it depends on the person employing which method is more suitable for him or her.

| 0 comments

Week Four: Sinusoidal Steady-State Analysis Part I

Sabado, Disyembre 6, 2014 | by Unknown

Nodal Analysis

  • Since KCL is valid for phasors, we can analyze AC circuits by NODAL analysis.

  • Practice Problem 10.1: Find v1 and v2 using nodal analysis
Solution:

For more information, Watch an Example!

Reflection:
        The application of nodal analysis in ac is still the same with the method used in dc. The difference between the two is that in ac analysis, it contains complex numbers and phasor forms. I still find it confusing when it comes to conversions. But with enough practice, anyone can attain the expected results.

| 0 comments

Week Two and Three: Impedance and Admittance

Sabado, Nobyembre 22, 2014 | by Unknown

The impedance Z of a circuit is the ratio of the phasor voltage V to the phasor current I, measured in ohms Ω.
 
The admittance Y is the reciprocal of impedance, measured in siemens (S).
    Admittance

Formulas Used:

Watch This Videos On How To Solve    Impedance and Admittance.


Reflection:
          Once you memorize these important formulas, it will be easier for you to convert them which is necessary for solving unknowns in ac analysis. You also need to familiar with them to avoid confusion or interchanging.

| 0 comments

Week One : Sinusoids and Phasors

| by Unknown

Sinusoid
   -is a signal that has the form of the sine or cosine function.
    -are easily expressed by using phasors.

Why sinusoid is important in circuit analysis?
  -Nature itself is characteristically sinusoidal.

  -A sinusoidal signal is easy to generate and transmit.

  -Easy to handle mathematically


Phasor
  -is a complex number that represents the amplitude and the phase of a sinusoid.

   
      -provide a simple means of analyzing linear circuits excited by sinusoidal sources.




     For More Information, Please Watch This Video!
Reflection:
           I think it is very important to have a sufficient knowledge regarding this topic because sinusoids and phasors are fundamentally present in analyzing mathematical problems in ac analysis. Especially when were converting them in their reactance.

| 0 comments

REMINDER: The following recent entries will be considered as posts for SECOND SEMESTER.

| by Unknown

| 0 comments

Week Thirteen: First Order Circuit

Sabado, Oktubre 11, 2014 | by Unknown

First-Order Circuit

   - can only contain one energy storage element (a capacitor or an inductor). The circuit will also contain resistance.

Two types of First-Order Circuits:
1. RC Circuit
2. RL Circuit

Source-Free Circuits
  - is one where all independent sources have been disconnected from the circuit after some switch action. The voltages and currents in the circuit typically will have some transient response due to initial conditions (initial capacitor voltages and initial inductor currents). We will begin by analyzing source-free circuits as they are the simplest type. Later we will analyze circuits that also contain sources after the initial switch action.



SOURCE-FREE RC CIRCUITS 

Consider the RC circuit shown below. Note that it is source-free because no sources are connected to the circuit for t >0. Use KCL to find the differential equation:

                             
                          



SOURCE-FREE RL CIRCUITS

Consider the RL circuit shown below. Use KCL to find the
differential equation:
                                                           
                                                                     


Watch a Video using First-Order Circuit!




Reflection:
          During our lesson, I have learned more about capacitors and inductors. Capacitors are treated as open circuit in DC while inductors are treated as short circuit in DC. This will be the last topic for this semester and sometimes when I try to solve the problem, I always get confused. But once I have practice solving it, I find it more convenient.

| 0 comments

Week Twelve: Maximum Power Transfer Theorem

Linggo, Oktubre 5, 2014 | by Unknown

The Maximum Power Transfer Theorem

  
 -the maximum amount of power will be dissipated by a load resistance when that load resistance is equal to the Thevenin/Norton resistance of the network supplying the power. If the load resistance is lower or higher than the Thevenin/Norton resistance of the source network, its dissipated power will be less than maximum.


Watch a Video using Maximum Power Transfer Theorem!

Reflection:
  I've realized that Thevenin's Theorem is very useful since it is a component in Maximum Power Transfer Theorem and other circuit related problems.

| 0 comments

Week Eleven: Thevenin's Theorem Part II

Biyernes, Setyembre 26, 2014 | by Unknown

Thevenin's Theorem



Case 2: Independent and Dependent Sources.

          -If the circuit to be Thevenized has both dependent and independent source, the method described above cannot be used to find the Thevenin resistance. Instead, you must find the short circuit current, Isc (current through short circuit at terminals). Then the Thevenin resistance is given by RT=Voc/Isc.
                   
                       
         Example of Circuit Problem using Case 2


Another Case: Only Dependent Sources.
     -If only dependent sources are present, then the Thevenin voltage is zero, and the Thevenin resistance is determine by applying a test voltage Vtest and the terminals and determining the resulting current, Itest. The Thevenin resistance is given by RT=Vtest/Itest. (Likewise, for this third case, you can apply a test current and measure the resulting voltage).
         
 Example of Circuit Problem with Dependent Sources Only


Watch an Example using Thevenin's Theorem Case 2:



Reflection:
       Comparing Case 1 and Case 2, I find case 1 more easy than case 2. Since case 1 only involves Independent sources while case 2 involves Independent and dependent sources.


| 0 comments
Mag-subscribe sa: Mga Post (Atom)
SUBSCRIBE rss feeds
Wall-E